Double Pursuit Curves
– Aug. 19, 2019
In the previous blog post, I showed the 'double pursuit curve' for squares. Here are images for the other n-gons up and until the octagon. For every n-gon, the first image has iterations with ratio 0.1 and the second image ratio 0.01. There are a lot more iterations in every second image. The individual lines are rarely visible since there are so many of them close to each other.
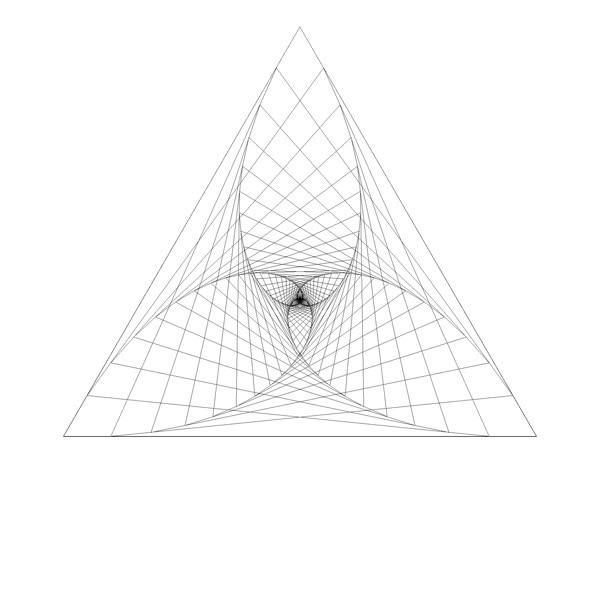

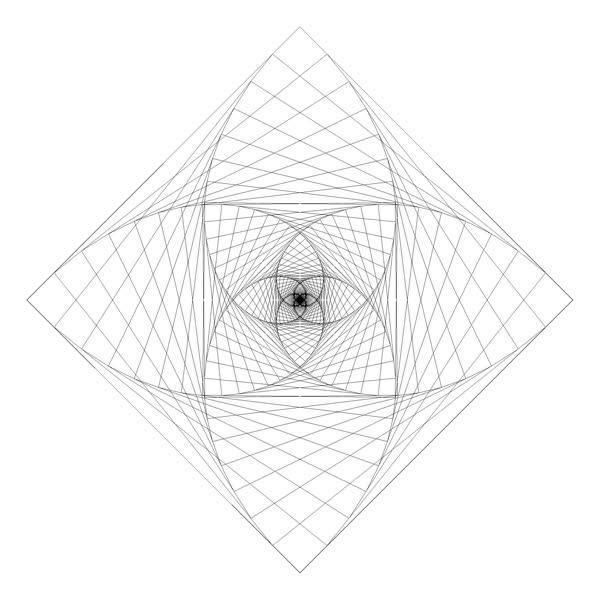
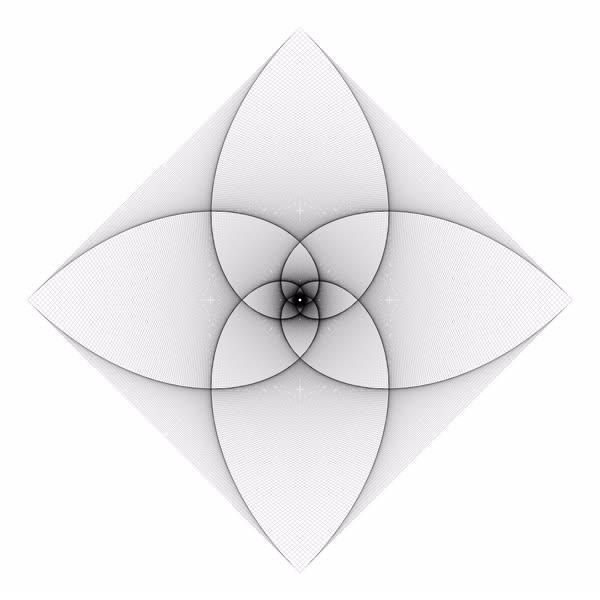
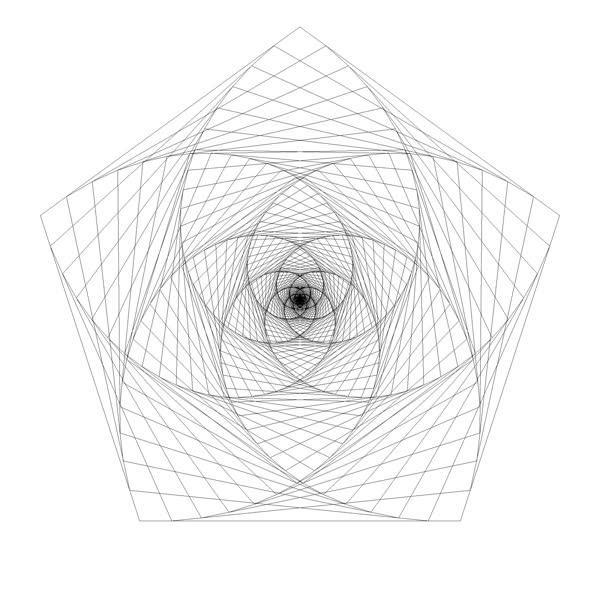
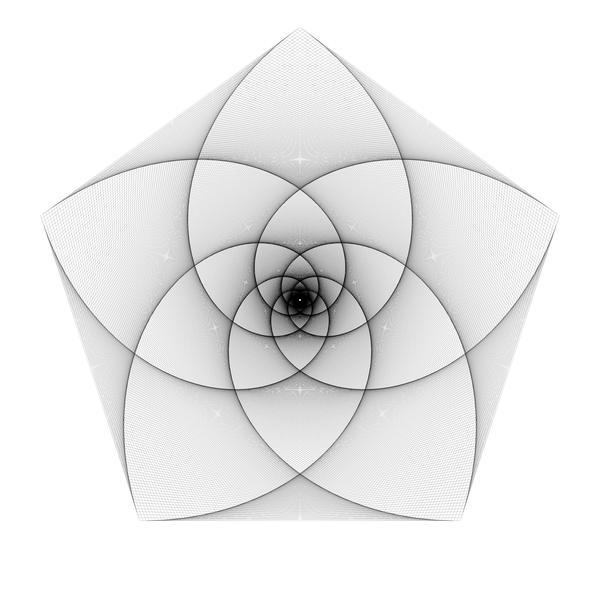
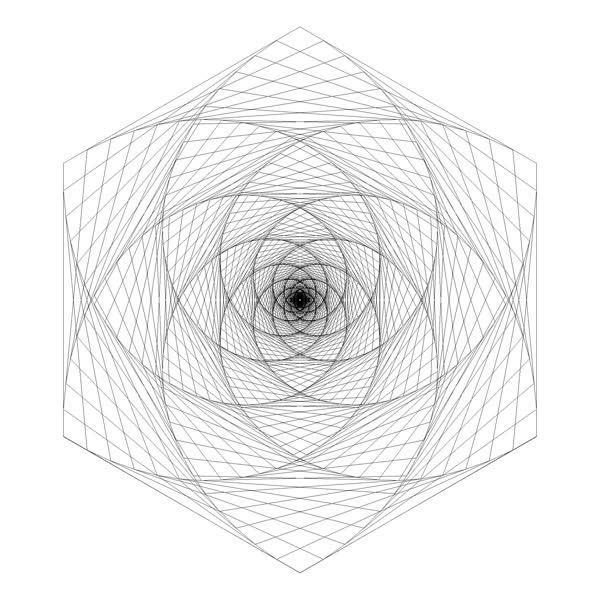
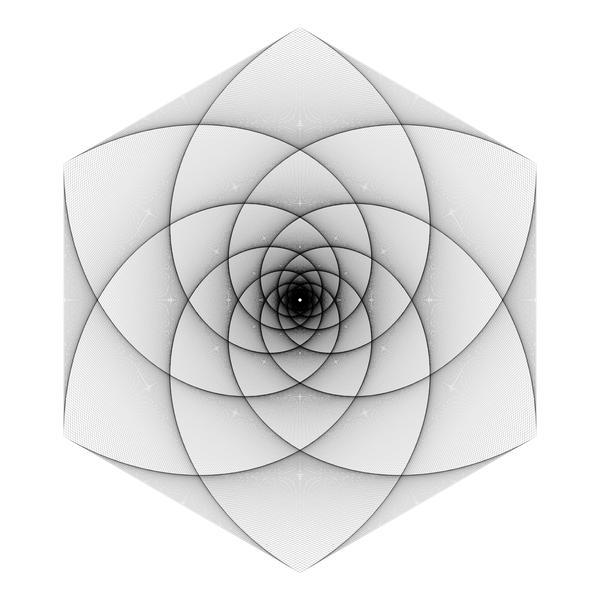
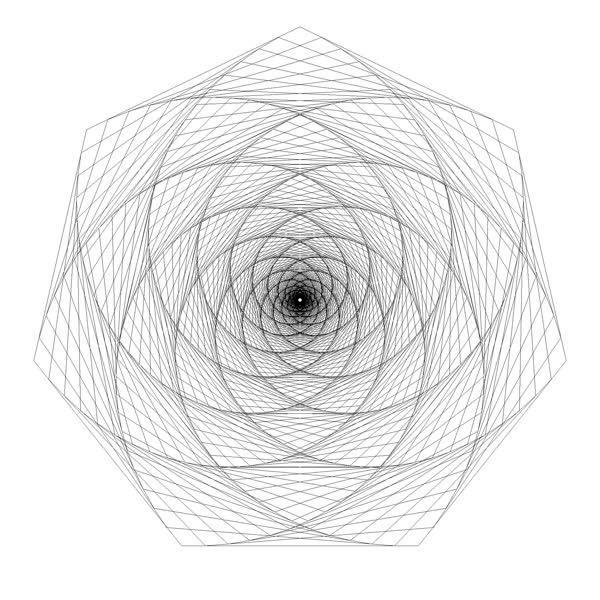



Here are animations for the triangle and the pentagon, with the ratio displayed.
In the following video, this is done for the first 6 regular polygons together. All images have 300 iterations, and the ratio goes from 0 to 0.02. In this part, the shapes look like flowers with n petals.
Instead of using the same regular polygon in two directions, I can also use two or more different polygons. Here are some examples.
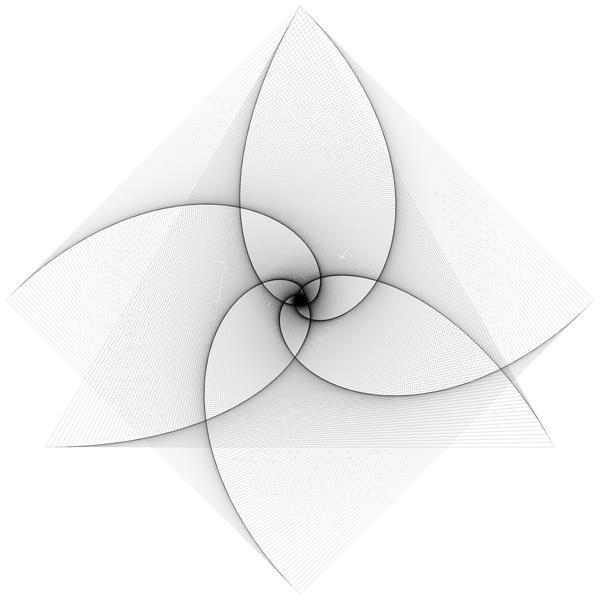 Triangle and Square
Triangle and Square

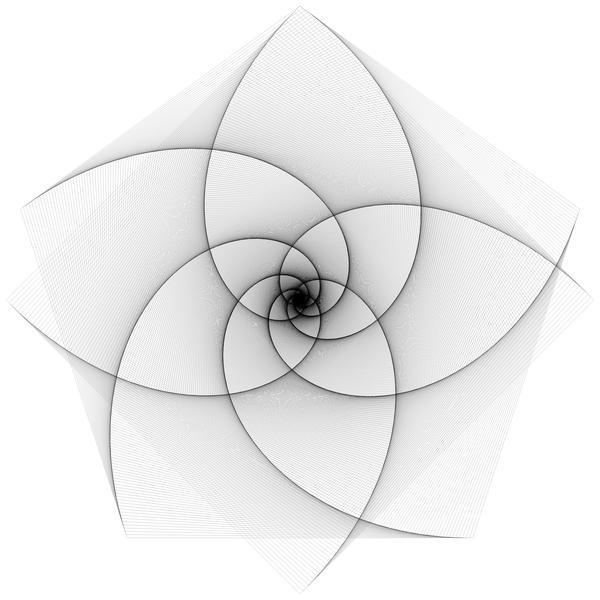 Square and pentagon
Square and pentagon
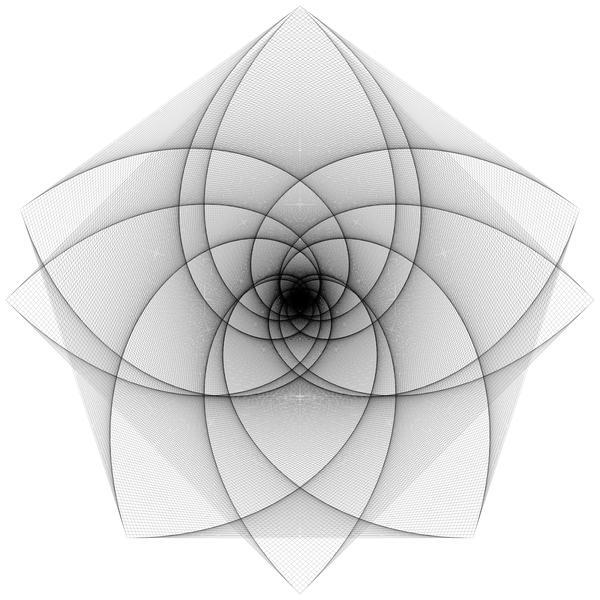
 Square and hexagon
Square and hexagon

 Triangle, square and hexagon in both directions
Triangle, square and hexagon in both directions

In the next image, the triangle, square and pentagon are all drawn in both directions. And in the second image this has been done for all n-gons until the dodecagon (12-gon). As you can see, I drew every polygon with one point fixed at the top center. That is why in the second image you can see many corner points of all the polygons on the bottom, but near the top, there are no corner points between the top point and the second 12-gon point.


Finally, I like to show what happens when you take 'many' corner points. There will be way more lines that overlap, and all those lines will create small gaps (mostly triangles) between them that become visible at certain ratios. This also depends on the line width in combination with the outer polygon size. In the next animation you can see what happens when two 24-gons iterate in opposite direction. Around the halfway point (ratio 0.5) a lot of interesting patterns appear quickly after each other. (Unfortunately, the quality after uploading is not good, if I ever figure out how to upload such content on YouTube with minimal quality loss, I will re-upload!)
Of course, many more variations can be made. I stop here, and continue with a different idea. But I am very happy to hear about other patterns that are based on this idea and of course similar work that has been done already. You can always send me links to interesting and relevant resources and I will update this post with those links.