Hiding text into an image

– Oct. 25, 2024

In this post I will describe what is perhaps the easiest way to embed a message into image data. My personal use case is to add the code that was needed to generate an image, into the image data itself. This means that I can deliver a single PNG file that was generated from code, which also contains that code inside the image.

Note that I keep the message in plain sight for steganographers on purpose. If you are looking to encrypt messages you might want to look for other resources in the field of steganography. I ignore image compression (until the notes at the bottom), since it is common for art outputs to use a 'lossless' image format, like PNG.

How digital images work

Digital images are built up from pixels. Every pixel has three color channels: Red, Green and Blue. There can also be a fourth channel for transparency, the alpha channel (the alpha channel will be ignored in this article). The value for each color channel can be represented by an integer in the range [0-255]. As an example: [255,100,10] has the maximum amount of red (255), 100 green, and a tiny bit of blue (10 / 255). These three values together represent orange.

In computing, values in the range [0-255] are represented with 8 bits in binary. So an image with three color channels has 3*8=24 bits for a single color value (a pixel). This is known as a 24-bit RGB color (and the variant with a fourth alpha channel would be 32-bit RGBA).

In the box above, you can change the color value by changing the integer values for R,G or B, or you can click on the colored bar to pick a different color. The bottom row displays three '8 bit values'. This is the color representation in 0's and 1's. For a digital image, these values are concatenated, so the selected value would look like this 111111110110010000001010: 24 values that represent a single color.

In fact, the entire digital image file is a sequence of such values. There is metadata near the beginning of an image file that indicates the file format, which color values to expect (24 bit versus 32 bit for example) and what the width and height of the image is. Whenever a program has to read such an image file, it knows it can take the data for every single pixel in chunks of either 24 or 32 bits.

Changing color values

There are many ways to manipulate images by changing color values. For example, we could add a blur filter, or sharpen an image (see 'kernels'). In this article, I want to focus on what happens when the color channel values change a small amount. Is a change of value 1 in every channel even visible? Remember there are 256 values per channel (from 0 until 255). For the three channels, there are 256 * 256 * 256 possible values that represent a single color. That means there are over 16 million colors possible for every single pixel on a screen!

In the section below, an image is displayed on the left. When you click one of the buttons, a modified version of the image will appear on the right. The color values in this right image will change based on your selected options. When clicking the rightmost button, only the very last bit of each channel value will be changed. This means that the color value will change with a value of 1. So 255 can become 254. Can you spot a difference in the new image?

Flip bits half of the time Flip every bit

Apply to all channels Apply to R channel only Apply to G channel only Apply to B channel only

2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰

The original image (double click to load your own image)

The manipulated image

The buttons are placed to represent the bits. 2⁰=1 and represents the last bit, the least significant bit. The leftmost bit is 2⁷ and represents the value 128. (more on binary counting here). When clicking any of these buttons, all bits from that button until the right will be flipped, and all bits left of the clicked button will stay untouched. By selecting from the dropdown, you can choose to flip every bit in that range, or only flip them 50% of the time. So when you click the 2⁷ button, all 8 bits will be adjusted. Did you expect the outcome in both cases (just flip every bit, versus, flip bits 50% of the time)?

It is interesting to see how much change is needed to make an image unrecognizable. There are also interesting effects appearing, when playing with those values. The main takeaway is that the least significant bit can be changed without it being noticed to most viewers. It can be set to any value we wish (0 or 1), wich means it can be set in a specific way to represent a meaningful text.

Extracting text from an image

To extract text from an image, we can examine the least significant bit of each color channel and combine them into a sequence, starting with the top-left pixel and ending with the bottom-right pixel (reading the RGB channels in that order for each pixel). The result will be a sequence of 0's and 1's. To map this with text characters, I choose to use ASCII, since it specifies a well known mapping between 256 text characters and the integers 0-255, or the bits '000000002' until 111111112

When applying this rule to any existing image, a non meaningful text will appear. This can be a random sequence of characters, but often it will display repeating values (because many images have regions with the same color). When clicking on the button below, the extracted text will appear next to the image.

The original Image (double click to upload your own)

Click to extract text from the image on the left

You can try this on any image you wish. And whenever you have an image with a meaningful text inside, you can come back here to extract it. The last image on this page is a png file containing the code.

Embedding text into an image

By using the above rules, we can convert any text into a sequence of 0's and 1's using the ASCII table. Every single text character will be converted to 8 bits. Whenever we encounter a character that is not present in ASCII, we can ignore it by replacing it by an empty character ' ' (space). This result can then be embedded into the image by setting those least significant bits accordingly.

Interestingly, this approach will not necessarily increase the image size. No data will be added, but existing bits will be changed. So it is essentially free to embed text into an uncompressed image. Another interesting observation is that on average, only 50% of the (least significant) bits have to be flipped. Half of them can be expected to be in the desired position already by pure chance. We want to encode either 0 or 1, and their value is already either 0 or 1.

* Note: the approach I use will copy the image data onto an html canvas, after which a new PNG file will be constructed from that canvas data. It seems that this new image does in fact become larger in file size, and I suspect this has to do with this particular way of copying the image data, and not with flipping the bits. When I compare the same image with a small or a very large text hidden inside it, the final result has roughly the same size.

For a single pixel value (the actual visible color), we can expect that:

• 12.5 % of all the pixels will stay unchanged. (1/8)
• 37.5 % of all the pixels will change a unit 1 in a single color channel. (3/8)
• 37.5 % of all the pixels will change a unit 1 in two color channels. (3/8)
• 12.5 % of all the pixels will change a unit 1 in all three color channels. (1/8)

This means that 50% of the pixels either do not change, or change by 1/16millionth of a color value (1/2563). You can go back to figure 1 to apply changes of 1 in any (or all) channels.

Note that all percentages mentioned above are about the part of the image pixels that contain the message, which is typically a few top rows. All other pixels will not be altered at all, which is typically the largest part (99%!) of the image. As the next section describes, it turns out that images can contain enormous amounts of text data.

I made this GitHub page, where you can do both operations: embedding data into an image and extracting the message from an image. It uses a 'stop identifier' and has a default limit on the amount of characters it will read from an image. The source code can be seen here.

How much text can be embedded?

For the strategy of flipping only the least significant bit, there are 3 bits of information in every color pixel. A text character takes 8 bits (since we use the ASCII table), so we need 3 pixels before we have enough space to embed a single text character. More precisely: every 2⅔ pixel values contain a single text character. Below you can specify a width and height and calculate how much text could be embedded in an image with those dimensions.

Note that a 1,000 x 1,000 pixel image already has a million pixels, and can contain 375 thousand (!) text characters. That is a fairly small image, yet it can contain the content of an entire book. An image made with a smartphone has a typical image dimension of 4000x3000 (12MP), which can contain over 4 million text characters (if it would not use a compressed image format)!

Things to keep in mind

• This only works for PNG files.
• The message will be lost whenever the image will be compressed or resized. The described approach only makes sense if you produce an image output that will not be modified, for example a final artwork release.
• There are alternative ways to store information in the image headers / tags, which means you do not have to fiddle with the actual image data. For the in-browser artworks, handling the image headers seems more challenging to me than handling the image color data. Also keep in mind that storing the code or a message in the image headers will increase the image file size.

The README on GitHub has a few more remarks.

My personal use case

I make algorithmic art, where I write code that produces a visual output. I have used the Python programming language to produce PNG files, but recently I am mostly generating art in the web browser. Below you can see an HTML document that produces a visual artwork. It contains some HTML (markup language) that defines a web page with a canvas, and there is JavaScript code that draws the art. The code on the left produces the image on the right.

<html><head></head><body style="margin:0;"> <canvas id="C" style="width:100%;" width="3000" height="1500"> <script>//CC BY-NC 4.0 www.josvromans.art A=window.requestAnimationFrame;C.width=W=3000;C.height=H=1500;X=C.getContext('2d');D=document;FN='aTtRaCtIoN'; L=(t='')=>D.title=t+FN;S=660239;R=_=>{S^=S<<13;S^=S>>17;S^=S<<5;return((S<0?~S+1:S)%999)/999} X.fillStyle='#fff';X.fillRect(0,0,W,H);X.globalCompositeOperation='multiply';X.globalAlpha=.1;P=[]; for(let k=500;k--;){l=[[1,10],[2,20],[2,5],[4,5],[4,5]][R()*5|0];x=240+R()*2520;y=140+R()*650;r=H/9;P.push([]);for(let i=0;i<l[0];i++){P.at(-1).push([(R()-.5)*r+x,R()*r+y])}}x=0;y=0;i=pi=0;T=(a)=>{L(['[ / ] ','[ \\ ] '][R()*2|0]);for(an=6000;an--;){if(i%10<1){pi=(pi+1)%P.length}r=P[pi][R()*P[pi].length|0];x+=(r[0]-x)/1.9;y+=(r[1]-y)/1.9; X.fillStyle=['#000','#de3','#FC0','#F90','#F60', '#C60', '#930', '#A0522D','#FF6'][pi%8];(x/249|0)%2&&(y+=200);X.fillRect(x,y,2,2);i++}i<5*10**6?A(T):L()};A(T);</script></canvas></body></html> The input (code)

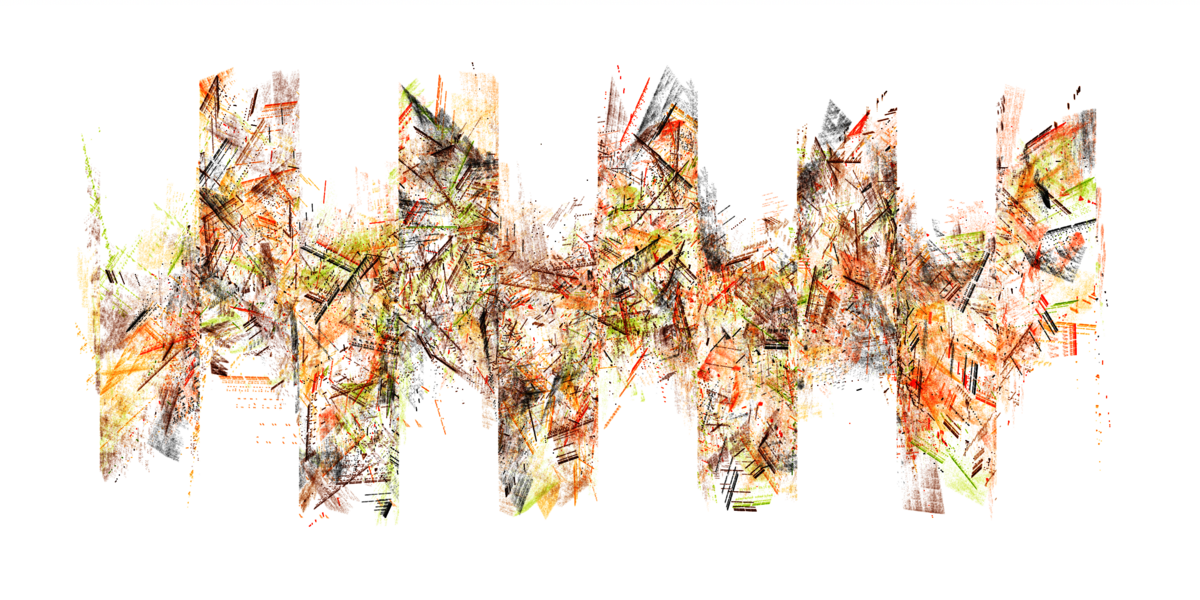The output (image)

You can run this in your own web browser by copying the content on the left, and save it in a text file as a HTML file, and then double click on the saved file to open it in the web browser. Alternatively, you can look at it here: here in case you like to inspect the code that generates the image.

My art contains two different things: the code (the algorithm) and the image output. Sharing just one of these two feels suboptimal to me. I could share just the code alone, which is really cool, as it would demonstrate how a bit of text characters can generate a visual output. The drawback is that to most viewers, a blob of text (code) does not look appealing at all, and it might not be straightforward how to turn the code into an image. So it seems that sharing an image file is a must.

When sharing the image alone, it gets lost that it has been made by handwritten code (in my case). So I want to share both, but ideally not as two seperate files, as that would introduce the challenge of connecting those two things. How would they reference to each other, and how to guarantee that they will be kept together?

So this is why I like the idea of merging those two things into one entity. For everyone who just likes the visual output, the image is there to look at. For anyone who likes to investigate how it's made, the code lies inside the image file. The image is the natural thing to display on a website, and everyone who is not aware of the code can still enjoy the image similar to how they would handle any image.

I believe that for handwritten algorithms, it is a unique strength to share the code with the output. The code can undeniably demonstrate that the artwork was generated from that code (and nothing else). This is especially relevant today, as there are countless software applications and libraries that might have been used to generate images, as well as AI and LLM models that could have been trained on unknown data. None of this might matter when you enjoy and judge images by appearance alone. But as soon as you like to know how an image was generated, it will be a unique feature to find the exact code inside the image. At least I hope it will be appreciated by future 'technical art historians', who like to investigate how an image was made.

For the code applies that the code can produce the art. A normal image output however, cannot produce the code. Using this approach, the image output can actually hold the code that was needed to generate it. This approach turns the digital image into a self-contained loop between the creative process and the final output image.

More use cases

Besides the HTML/JavaScript example, this can be used for anything really. You could add things like copyright notices, artwork description, artists name and website, resources used, etc.

For the 'generated by code' approach, any language or tool could be used, for example with the software or libraries used included as a comment. Any art output that was generated with Python code, for example within the Blender software, could contain the Python script and the version of software used.

Instead of matching the exact image output, this technique also allows publishing a small and low resolution PNG output. But in that low resolution output file hides the code that can generate high quality outputs. This could be an approach where the viewer is challenged to run the code live in their browser.

Digital watermarking can be a way to protect your art, or to just add your mark as a best practice.

One Last Trick

The approach I described for my personal use case would take an existing image, then modify it by adding the code into the image data, which would create the final output. So basically I end up with two 'final' images which are not exactly the same:

1. One image that does not have the code included yet, but it has all pixel values exactly as intended (generated by the algorithm).
2. One image that does have the code included, but it has some very small changes in pixel values, so it is actually slightly different from the original image.

Even when it is not visible for most humans, doing an 'image diff' will show exactly that there is something different. One could argue that image 2 is not exactly the original output from the algorithm.

This can be resolved by embedding the source code into the image before exporting the image to PNG. For my example in HTML/JavaScript it is possible to retrieve the source code of the current web document. So after the algorithm creates the entire image on the digital canvas, one final step will be taken to embed the source code into the color data. Whenever the canvas will be saved as a PNG, it will already contain the code to generate an exact copy of itself.

For this approach, it means that the image can be derived from the code, and the code can be derived from the image.

The code snippet here can do just that. This can be used in the development process, where an artist can save any iteration of their work as a PNG file, without ever losing the code that generated the image.

Some notes and final thoughts

This entire writeup is focussed on a raster based lossless image format (for example PNG). Digital color is a complex topic, and it is hard to do a write up without considering compression, color depths, image formats, color gamuts, color spaces etc. I tried to stay away from it all to keep things simple. There are certainly other digital image formats that do not behave as I described, for example vector based formats like SVG.

When exploring this approach for final art outputs, it might be interesting to think about mentioning it in the image tags or metadata. The metadata could say something like: "This artwork was generated by code, the least significant bit of the image data contains that code."

A checksum can be used to keep track if an image file is in its original, unaltered, state.

You can definitely use the last 2 significant bits, the last 3 significant bits, or adjust the alpha channel, so you can store even more information in an image (with more visual changes).

Even though the described approach does not work for compressed images, there is still potential to hide information in such images. Simply because messages can be small, and the image data is large. Steganographic methods can account for known compression techniques (some of them work with predictable 8x8 blocks). A precise GPS location, like a geohash needs only 11 characters. So even when compression means that 1000x less information can be embedded, there is still space to embed such a location in practically any image. It is also worth noting that more robust steganographic methods typically add information to the message itself to enhance reliability, for example using error-correction codes.

Subscribe

If you enjoyed this, you can subscribe on this page and get notified whenever I publish a new article.